| No.6 题目:用*号输出字母C的图案。
题目分析
本题为经典的使用某种特定符号绘制相关图形,此处要求使用 “*” 输出字母 C,在编程竞赛中本类题目也是经典的题型之一,由于要求输出的字母符号较为简单,我们直接看代码:
#include<stdio.h>
int main(){
printf("******\n");
printf("*****\n");
printf("****\n");
printf("***\n");
printf("***\n");
printf("***\n");
printf("****\n");
printf("*****\n");
printf("******\n");
}
|No.7 题目:题目:输出9*9口诀。
题目分析
在本题中,要求我们输出9×9的乘法表,重点考察的则是对于 for循环 应用,在编写本题的代码时,有很多同学想到的确实是for循环,但是他们最终输出的只是单纯的一行一项的“9×9乘法表”,还有一部分小伙伴提交之后通过率为0,于是找到博主抱怨评测系统太“垃圾”哈哈哈哈哈哈哈哈哈哈哈,这个时候博主的表情一般是

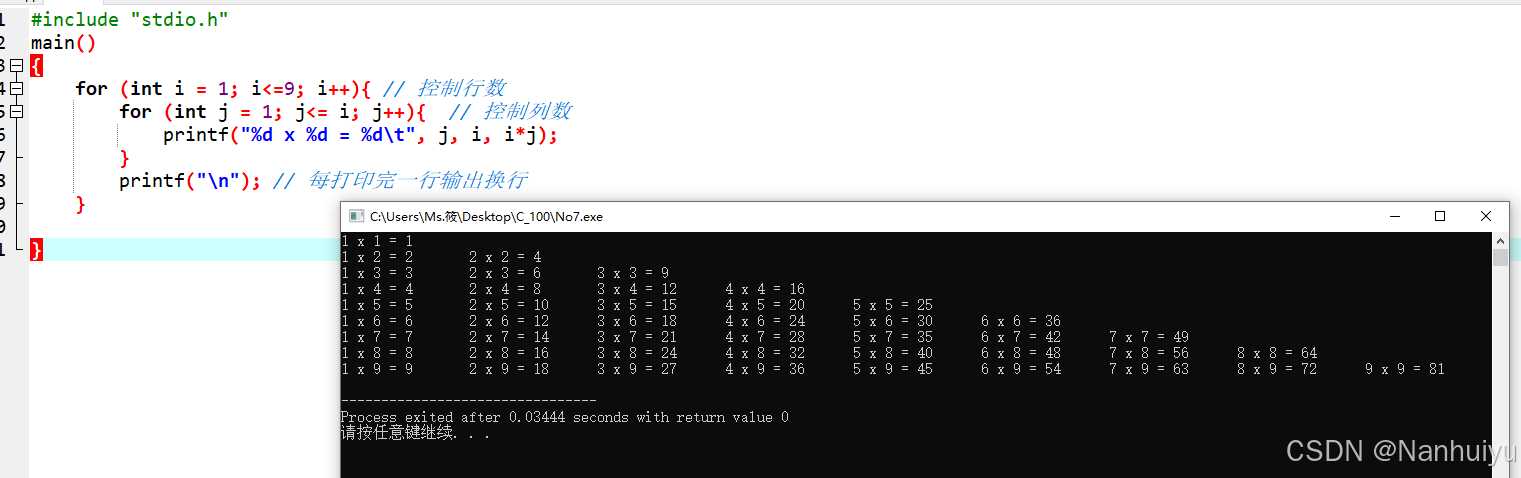
其实题中所要求的并不是这样的“9×9乘法表”,而是:

当然框框不用,只需要有这样的层次结构就行,既然了解了前因后果,那么如何用for循环来实现这个效果呢,单个循环的效果我们已经知道了,显然用来实现这样的表格结构是不太可能的,因此,本题中我们应当考虑使用的是 嵌套循环
那么基本方向确定了,嵌套循环有应该怎么做呢?显然这个表格每一行每一列的数量都是不一致的,这里就需要同学们掌握一个嵌套循环的“特性”知识点:外循环控制行数,内循环控制列数 ,即本题 外部循环自1到9 ,至于内部循环,稍微观察一下就能发现,其实 每一行的列数其实等于其所在行的行编号 ,至此,本题的所有核心要点就全部罗列出来了,接下来我们看代码:
#include "stdio.h"
main()
{
for (int i = 1; i<=9; i++){ // 控制行数
for (int j = 1; j<= i; j++){ // 控制列数
printf("%d x %d = %d\t", j, i, i*j);
}
printf("\n"); // 每打印完一行输出换行
}
}
| No.8 古典问题:有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月 后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总数为多少?
题目分析
本题将是我们学习C语言以来至今遇到的一道比较大的坎,当然就本题来说其实并不难,但是如果有小伙伴以后希望进军编程竞赛方向的话,应该可以看到很多关于本题的变体,考虑到初学,我们只使用 for循环+简单的递推 实现,这里只求前20个月中每一个月的兔子总数并打印,我们先来解析一下本题的数学逻辑:
1. 问题建模
初始条件:第 1 个月有 1 对幼年兔子(记为 $F(1) = 1$)。
生育规则:
– 幼年兔子需 2 个月成熟,从第 3 个月起每月生 1 对兔子。
– 成熟兔子每月持续繁殖,永不停止。
– 无兔子死亡,种群无限增长。
2. 递推关系推导
- 第 1 个月:1 对(幼年,未成熟)。
- 第 2 个月:1 对(仍为幼年)。
- 第 3 个月:1 对(成熟)→ 生 1 对 → 总数 $1 + 1 = 2$ 对。
- 第 4 个月:原 1 对继续生 1 对,新生的 1 对未成熟 → 总数 $2 + 1 = 3$ 对。
- 第 5 个月:原 1 对生 1 对,第 3 月出生的 1 对开始生 1 对 → 总数 $3 + 2 = 5$ 对。
递推公式:
$$
F(n) = F(n-1) + F(n-2), \quad (n \geq 3)
$$
解释:
– $F(n-1)$:上个月的兔子总数(所有兔子存活)。
– $F(n-2)$:两个月前的兔子总数(这些兔子现在已成熟,每对生 1 对新兔)。
那么如果已经接触过数列这块知识的小伙伴们应该能很快反应过来,其实这个增长规律在数学中被称为 斐波那契数列 ,当然你也可以称呼他为 兔子数列 ,这里可以为小伙伴们提几个名词,是专门用于解决这类编程问题的方法:一个是递归与递推,一个是滑动窗口,一个是剪枝,有兴趣的小伙伴可以去学习一下哦,如果觉得理解起来很艰难也是完全没有关系的,作为初学者在这里留一个印象即可。
那么言归正传,本题将使用循环实现求前20个月的兔子数量变换,由于基本逻辑实现起来还是比较简单的,在看代码之前,我们先来说明一下代码中变量的关系:
f1:前第一个月的兔子数量
f2:前第二个月的兔子数量
f3:当前月的兔子数量
f1 f2 f3 -> f1 (f2->f1) f2 (f3->f2) f3
2 3 5 -> 3 5 ?
如果对于上面的f1、f2、f3的关系变化不太理解的小伙伴,您可以拿出纸笔,模拟一下这个递推关系,学习斐波那契数列的关系,然后写出题中的数列,在数列下写上f1、f2、f3,并不断向后移动这三者的位置,您应该会有新的理解,现在,我们直接看代码:
#include<stdio.h>
/*
f1:前第一个月的兔子数量
f2:前第二个月的兔子数量
f3:当前月的兔子数量
f1 f2 f3 -> f1 (f2->f1) f2 (f3->f2) f3
2 3 5 -> 3 5 ?
*/
main()
{
long f1, f2, f3=0; // 后期的数量将会比较大,因此这里我们直接 long而不是用int
f1=f2=1; // 初始的兔子数量
for(int i=1;i<=40;i++)
{
f3 = f1 + f2; // 累计求当前月的兔子数量
f1 = f2; // 为了求下一个"当前月"的兔子数量,这里向后递推f1和f2的值
f2 = f3;
printf("%12ld", f3); // 输出当前月的兔子数量
if(i%4==0) printf("\n"); // 控制输出,每行四个
}
}
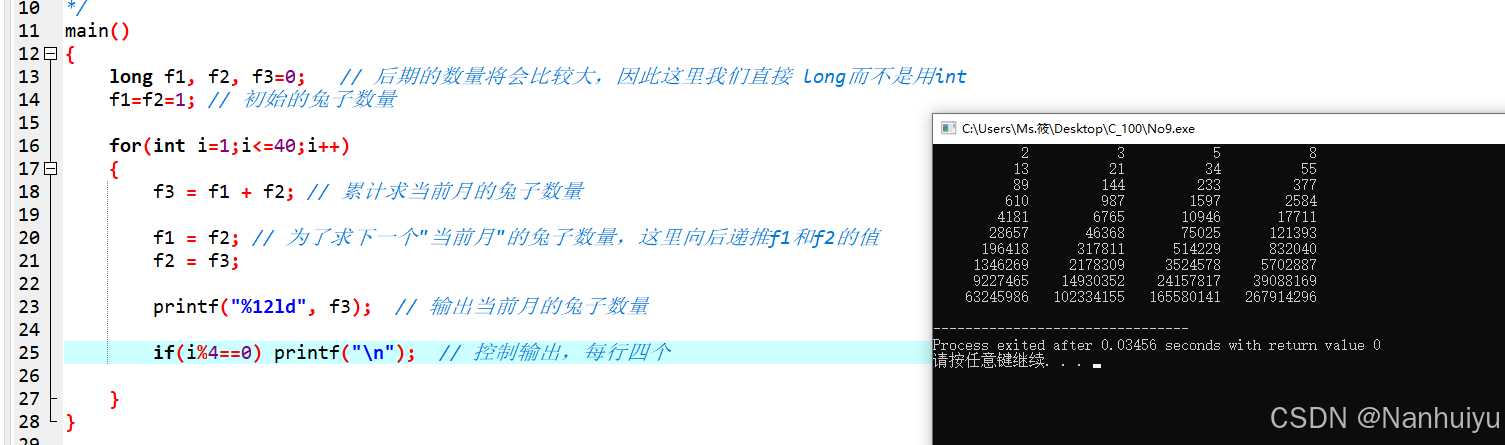
以上是通过for循环实现的部分,如果有学习超前的同学,已经学习到了函数调用和递归这块的内容,可以试着用递归的方式实现一下本题的逻辑哦,并尝试求一求月份在40之后的兔子数量,并对比上述使用递推求解相同月份的兔子数量的方法,相信你对于递归的一些优势劣势也会有新的理解,如果您对使用递归的方式实现有困难,可以参考一下的代码,以下代码使用 递归 实现对兔子序列的求解:
#include <stdio.h>
long long rabbit_count(int n) {
if (n == 1 || n == 2) {
return 1; // 前两个月兔子数都是1,对应的for循环方式实现中的f0, f1, f2,此后开始求f3
}
return rabbit_count(n - 1) + rabbit_count(n - 2); // 递归的求 第n-1个月 和 第 n-2个月 的兔子数量,二者之和为 第n个月 的兔子数量
}
int main() {
int months = 45; // 计算前 45 个月的兔子数
for (int i = 1; i <= months; i++) {
printf("第 %d 个月兔子总数: %d\n", i, rabbit_count(i));
}
}
| No.10 判断101-200之间有多少个素数,并输出所有素数。
题目分析
在本题中提到了 素数 ,这是一个数学概念,我们先来解释这个概念:
素数,又称质数,是数学中一类重要的自然数,其定义如下:
- 定义
素数是大于1的自然数,且除了1和它本身外,没有其他正因数。换句话说,如果一个数只能被1和它自身整除,那么它就是素数。- 关键点
- 必须大于1:
- 最小的素数是2,而1不是素数(因为它只有1个因数,不满足“大于1”的条件)。
- 没有其他因数:
例如,7是素数,因为它只能被1和7整除;但8不是素数,因为它还能被2和4整除。
其在了解以上概念之后,我们来聊一聊如何实现判断一个数是否为素数,其关键点就在于 “除了 1 和 本身 之外没有其他的因数” ,那因该如何判断他是否含有其他因数呢?
我们知道,在C语言中有一个运算符 % ,若 ab = c ,则有 c%a=0 或者 c%b= 0,因此我们便可以通过 在循环中 这个逻辑来实现对素数的判断。
由于代码实现起来难度不大,因此我们直接看代码部分:
#include<stdio.h>
bool is_pri(int num){ // 判断传入函数的数字num是否为素数
for (int i=2; i<num; i++){
if (num % i == 0){ // 根据 ab=c,则c%a=0或c%b=0,若出现这样一个非1和非num本身的数,则表示num非素数
return false;
}
}
return true; // 在1到num范围内并没有找到能实现c%a=0或c%b=0的a或b,则num为素数
}
int main(){
int cnt=0;
for (int i=101; i<201; i++){
if (is_pri(i)){
printf("%d\n", i);
cnt ++;
}
}
printf("cnt: %d\n", cnt);
}
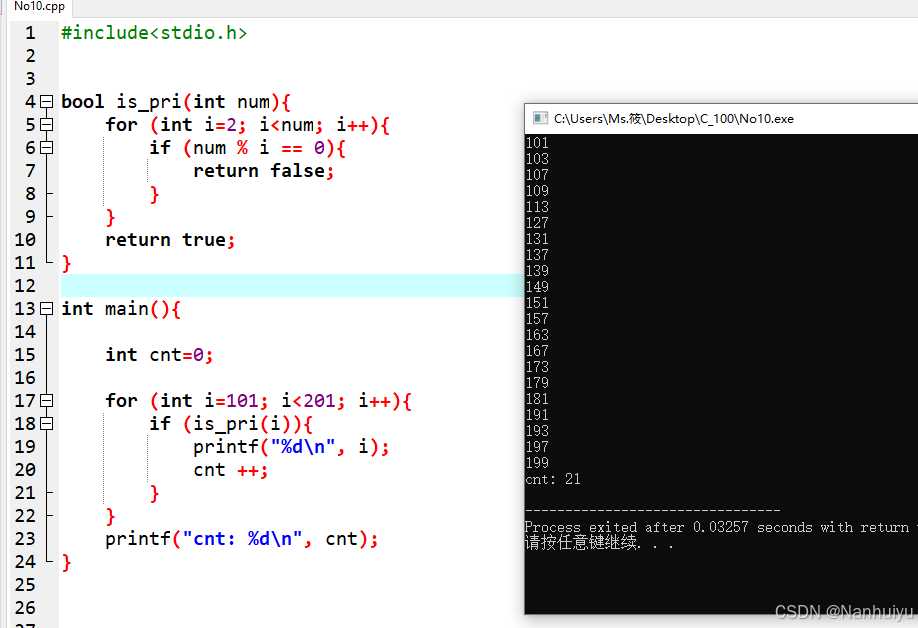
在本处,判断素数的部分被封装在了一个 bool类型 的函数中,在for循环中调用本函数,以达到简化代码主体部分,使得代码整体结构清晰、便于后期维护等特点,在平时的代码编写过程中,同学们也可以尝试将一些功能模块封装成函数放在main函数的外部,这种方式在实际开发中也是非常常用的哦!
仅从最终的结果来看,本题的结果是没有问题的,但从逻辑方面来说,本题的解法还是存在小小的问题,其实,在判断一个数是否为素数时,只需检查到其平方根($√(num)$),这背后的原理可以通过因数对的对称性来解释:
因数的成对性
假设一个数 (n) 不是素数,则它至少有一对因数 ((a, b)),满足:
$n = a \times b \quad (a \leq b)$
其中:
– a 是较小的因数,
– b 是较大的因数。
关键观察:
– 当 a 增大时, b 必须减小。
– 最大可能的 (a) 是当 (a = b) 时(即 (a = b = √n))。
如果 (a > √n),则 (b < √n),这与“ a 是较小因数”矛盾。
因此,所有可能的较小因数 (a) 必然小于等于 (√n)。
在了解以上内容之后,针对No.10的第一个优化方案就出来了,除此之外,我们还可以从判断一个数的因素出手,毕竟不太可能在 (1, num) 这个范围内所有的数都是目标数字num的因数(当然如果这个数字够小比如2还是有可能滴), 换句话说,一个数的因素不太可能在一个范围内完全保持连续,那么应该如何 加快程序在判断一个目标数字的所有因数的速度 呢?这是本题的第二个优化的方向
上述两个方向实现起来的难度并不大,只是可能需要您去额外学习一些内容,相信 作为初学者但是动手能力强又爱自己实践码代码 的你们肯定愿意亲自动手去尝试实现这两个方向的对吧!
此外,我们根据此前了解到的素数的概念,知道素数也是不太可能在一个较大的范围内保持连续分布的,因此,我们可以不对待求范围内所有的数字进行判断,而是专门判断那些既有可能是素数目标数字,这就是本题的第三个优化的方向,当然也是本题三个优化方向中难度比较高的方向,有小伙伴可能会比较疑惑,难道素数的分布还有规律吗?
有的有的兄弟有的像这样的方法还有九种

虽然这种方法并没有完整的 “充要” 的关系,但是这种方法却可以进一步将素数的分布范围进行压缩,但是由于这种方法说明起来比较繁杂,详情请看我的个人博客文章:[NOIP2012 普及组] 质因数分解–一题速解质数问题,不过本文是通过python实现的上述逻辑,有需求的小伙伴可以私信我,我将为您提供c语言实现的版本。
那么以上就是本期 C语言从初识到竞赛精通 No.6-No.10 的全部内容了,如果您在阅读本文的过程中有所收获,或者有任何宝贵的建议和想法,欢迎通过邮箱、微信或者留言等方式给我留言交流,您的每一次建议都将是我前进的动力!









