原题传送门：3.拼正方形 – 蓝桥云课

问题描述：

小蓝正在玩拼图游戏，他有 7385137888721 个 2×2 的方块和 10470245 个 1×1 的方块，他需要从中挑出一些来拼出一个正方形，比如用 3 个 2×2 和 4 个 1×1 的方块可以拼出一个 4×4 的正方形，用 9 个 2×2 的方块可以拼出一个 6×6 的正方形，请问小蓝能拼成的最大的正方形的边长为多少。

答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

问题分析

本题较为简单，这里我们选择使用二分搜索作为解决本题的核心算法，已知的条件是：

• 1，有两种不同数量不同变长的正方形

• 2，所求最后图形为正方形，但要求其边长最大

从数学角度分析，设正方形的边长为 n，则它的总面积为 ，由于一个 2×2 的方块占 4 个单位面积，因此可优先使用 2×2 的方块，设使用了 x 个 2×2 的方块，它们的总面积为 4x 。

剩余需要用 1×1 方块补充的面积为 ，这个值不能超过 1×1 方块的数量。

目的便是：找到最大的 n，使得：

n^2 ≤ 边长为2的方块提供的面积 + 边长为1的方块提供的面积

即：

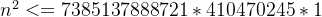
以上便是本题比较直观的数学语言表示，到这里我们不妨做一个比较极端的假设：

假设均使用 2×2 的方块堆叠成最终的这样一个正方形，则用上的2×2方块的最少数量应当是：

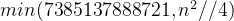
为这部分值赋予变量名：used_two_by_two

此时我们再将所有已用的 2×2 正方形假设成为4个 1×1 的正方形叠加而成，为了达到最终的最大正方形的效果，则现在应当做的是，使用足够数量的 1×1 的正方形去填补剩下的可能存在的“空隙”，示意图如下：其中绿色部分为可能需要使用 1×1 的正方形去填补的部分

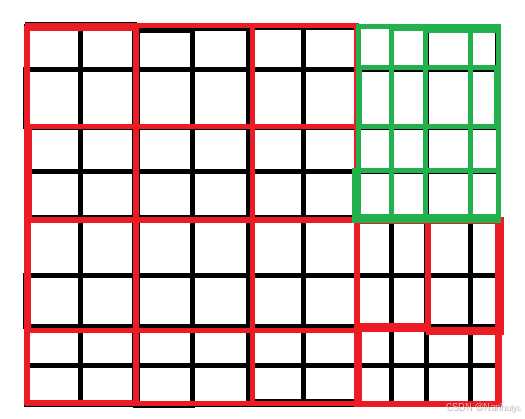
记 1×1 的正方形填补的部分为 remaining_area，则这部分的数量应该为：

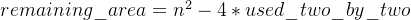
接下来我们应该做的事情就是：判断 remaining_area 是否小于等于 1×1 方块的总数。本条件也是二分搜索进行的核心

总的逻辑分析如上，既然确定使用二分搜索，那对什么元素进行搜索呢？这里毫无疑问是正方形的边长了，那搜索的范围应该是什么呢？二分搜索嘛，你知道的呀，二分搜索的时间复杂度嘛，你知道的呀

因此，我们同样假设两个极端，首先由题可知，最小的能拼成的正方形为边长 1×1 的正方形，则二分搜索的左边界为1；其次，我们假设所有的小正方形均被用上，则最后的大正方形，其面积为：

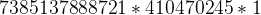
那么其可能的最大边长则是：

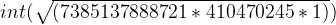
到此，二分搜索的左边界与右边界都确定的了，接下来就是编程时间！

代码描述

由于二分搜索的代码实现起来比较简单，所以这里不对代码做额外的详细讲解了，有需要的同学可以评论区或者私信留言，这里需要注意的是，二分搜索的退出条件，应当着重考虑实际需要的1×1的正方形数量和题中所给的最多的正方形数量

有同学提问对于本体代码中二分查找边界mid和left的问题，请注意，本题中小于和等于条件不能放在一起判定，因为我们先考虑利用的是2×2的大方块，其中2×2的大方块的使用数量一定在题目的限制数量之内，但是1×1的小方块可能由于二分查找的移位性质导致超出实际限制数量，也就是说left是一定合法的的，但是mid实际可行范围可能要大于left，因此本题并不能尝试在remaining_area = max_one_by_one时返回mid，否则二分查找将再次执行一次导致实际结果大1，即，将此条件合并到 remaining_area <= max_one_by_one 中。这种合并将会导致以下问题：

• 当 remaining_area = max_one_by_one 时，1×1的小方块数量已经到达到题目限制，但是由于二分查找设定的条件是remaining_area <= max_one_by_one，此时代码将会继续尝试更大的 mid 值，但由于 mid可能已到达题中限定的最大值，后续迭代可能因 remaining_area > max_one_by_one 而错误地缩小右边界。

完整的代码表述如下：

def max_square_side():
    max_two_by_two = 7385137888721  # 2×2 方块数量
    max_one_by_one = 10470245       # 1×1 方块数量

    # 设定合理的二分查找范围
    left, right = 1, int((max_two_by_two * 4 + max_one_by_one) ** 0.5)

    while left < right:
        mid = (left + right + 1) // 2  # 取上中位数，防止死循环
        total_area = mid * mid  # 需要填充的总面积

        # 计算最多能使用的 2×2 方块数量
        max_used_two_by_two = min(max_two_by_two, total_area // 4)
        remaining_area = total_area - max_used_two_by_two * 4  # 需要补充的 1×1 方块面积

        if remaining_area < max_one_by_one:
            left = mid  # 继续尝试更大的 n
        elif remaining_area == max_one_by_one:
            return left
        else:
            right = mid - 1  # n 太大了，尝试更小的 n

    return left  # 返回最大合法的 n

print(max_square_side())  # 输出最大边长

运行结果：

提交官网：

到这里本题就结束了，那么关于这个题目，同学们是否还有更多想法呢？对于二分查找的理解是否已经跳出模板达到随心所欲不逾矩的程度了呢？

如果您在阅读本文的过程中有所收获，或者有任何宝贵的建议和想法，欢迎通过邮箱或是微信等方式给我留言交流，您的每一次建议都将是我前进的动力！在此，博主斗胆向您提出一个小小的请求，如果您觉得本文给您带来了一丝启发，不妨动动手指，给予一点点鼓励。万水千山总是情，您的打赏，哪怕只是 0.1 元，也是对博主莫大的支持！（悄悄告诉您，博主正在为服务器众筹中 (×﹏×)，您的每一份心意都将助力博主走得更远！）感谢您的慷慨，愿我们的缘分如同这网络世界，绵长不断